We use Faraday's Law in integral form:
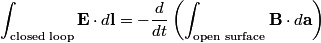 We choose to traverse the loop in a clockwise direction. We also choose the reference direction of the current 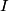 to be in the clockwise direction. Then, to be in the clockwise direction. Then,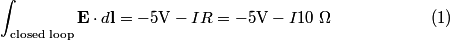 By the right-hand corkscrew rule, 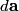 points into the page. Therefore, points into the page. Therefore, 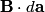 is positive. Therefore, is positive. Therefore, 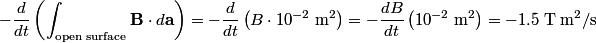 Therefore, 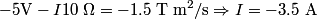 The minus sign indicates that the current is actually in the counterclockwise direction. Therefore, the answer is (B). |